Batch 2 - Class 103 - Pancake Sorting & Len Choa copy
Pre-Class Problem:
The Same Court Time
Basketball is one of the most popular team sports in this summer’s Olympic Games. The game is played with five players from each side on the court at the same time, and is played for four 10-minute quarters. The coach of the Brazil team has decided to give every one of her eight players the same court time. What scheme should she use to ensure this?
- Many ways to solve for this. One easy solution is 12345, 23456, 34567, 45678, 56781, 67812, 78123, 81234
- Another funny one is to forfeit!
- Another one is to have the coach play all through and then give each player two quarters!
Attendance: Smiti, Muskaan, Tishyaa, Khushi, Arnav, Anishka
Class Notes:
Pancake Sorting Problem
(Posed in 1975 by Jacob E. Goodman) The chef in our place is sloppy, and when he prepares a stack of pancakes they come out all different sizes. Therefore, when I deliver them, on the way to the table, I rearrange them so that the smallest winds up on the top, and so on, down to the largest at the bottom, by grabbing several from the top and flipping them over, repeating this as many times as necessary. If there are n pancakes, what is the maximum number of flips that I will ever have to use to rearrange them?
- Instructor Notes: Let kids think about the problem. Ask them to solve it for small numbers
- What is P(1)? P(2)?
- Can you figure out P(3) - Let kids work this out independently. P(4)?
- Let kids try for higher number of pancakes.
- Is there a pattern? Is there a method to figure this out quickly for a large number of pancakes?
- How does the complexity seem to grow?
- The number of flips required for 19 pancakes is only 22. But the most powerful computers have not been able to solve for 20 pancakes!
- Can you figure out a method which can get it done in under 2n steps?
- This is a class of problems which is called "NP-Hard" - there is no "easy" way that has been discovered to solve NP-Hard problems
- In 1979, some one showed that the maximum number of fipas required is (5n+5)/3 - Any guesses who was it?
- Bill Gates (with Christos Papadimitriou)
Can you demonstrate that their are an infinite number of prime numbers?
(was proved by Euclid in 300 BC)
Jokes:
- What did number 0 say to number 8?
- "Nice Belt"!
- Teacher: "What is seven Q plus three Q". Student: "Ten Q". Teacher: "You are welcome"!
- Competition: Can you come up with a meaningful mnemonic to remember pi (length of each word in the sentence represents successive digits of pi. Lets get started with "How I wish I could recollect pi easily today!"
- Note: pi = 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679
- In class we got to this

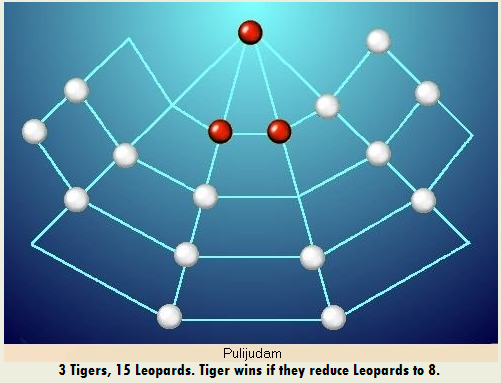
Len Choa - Leopard Hunting Game
.png)
There is a triangular jungle on which this game is played. The tiger starts at top of the grid. Leopards (total 6 in number) enter one at a time, from periphery of the jungle. Tiger's mission is to kill the leopards by jumping them. Leopards' goal is to surround the tiger, preventing escape. All leopards must enter before they start to move.
Play the game and devise a winning strategy.
Variants:
.png)
Homework
Find four different fractions, in each of which the numerator is one less than the denominator, so that when all four fractions are added together, their sum will be a whole number. There is more than one solution.
- Answer:1/2, 2/3, 6/7, 41/42 - Many other solutions
- Since each number is of form (n-1)/n which is 1-1/n, and since sum of all four is integer, it means that 1/a+1/b+1/c+1/d is an integer. The largest value of this is for a,b,c,d=2,3,4,5 which is 1.28, so the integer sum must be 1, and a must be 2. Hence 1/b+1/c+1/d=1/2. Now set b = 3 to find some solutions for c and d; then set b = 4 to find other solutions, and so on.
References: